第21話 δ 関数
構造解析における有限要素法も他の数値解法同様、結局は離散点(すなわち節点)での力の平衡方程式を求めることを目的とする。節点に働く作用力の代表は、構造物に発生した応力からくる内力と荷重からくる外力である。
ここでは外力の方に注目してみる。1要素の表面に作用する分布荷重に由来する表面力は次の通りである。
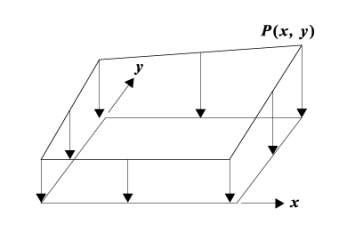
図21‒1 要素表面の分布荷重

ここに、N は変位関数よりなるマトリックスである。T は転置記号。積分は面積分である。
P は通常、荷重強度の分布を表す連続関数であり、分布荷重と呼ばれる荷重の場合は別段、問題なく積分は求まる。積分の結果は外力の等価節点力が求まることになる。
もし、要素表面内の1点にぽつんと集中荷重が作用しているような場合はどうなるのであろうか。ちなみに、節点位置に作用する集中荷重は別に問題はない。この場合は、最終的に求まっている平衡方程式の外力ベクトルの対応する項に直接、加えればいい。

図21‒2 要素表面内部に作用する集中荷重
もし、要素形状が単純に矩形であれば、上の問題は関係節点に直感的に割り振るような対処をされることが多いであろう。しかし、要素が歪んでいる場合、すなわち、積分領域が素直でない場合はどうなるのであろう。こんなとき、役に立つのがディラックの δ 関数である。ディラックの δ 関数(下は1次元の場合)とは次のような関数である。

ディラックの δ 関数を応用すると最初の式は次のように展開される。

ここに、ξp、ηp は集中荷重の作用点を示す無次元座標とする。
ディラックの δ 関数は、あらゆる工学問題の分野で利用される有用な関数であるが、これが登場したときは物議を醸したそうである。そのことは後で述べるとして、まず、それを使い出した張本人のディラックのことを少しだけ紹介しよう。
ディラック(Dirac;英1902-1984)は20世紀前半に綺羅星のごとく登場した天才物理学者達の一人で、その中でも極めて異例な才能の持ち主であった。元々、電気工学分野の出身者であった。20世紀物理の2大理論である相対性理論と量子力学を組み合わせた“ディラック方程式”を開発した功績で1933年には、これまた有名なドイツのシュレーディンガーとともにノーベル物理学賞を受賞している。彼は、ディラックの発言でなければ狂人の戯言として片付けられそうな奇想天外な予言をしたことで有名である。陽電子やモノポールの存在がそうである。
あまりに大胆な思考なので周りに受け入れられないこともあったが(モノポール[単磁極]などはいまだ発見されていない)、後にディラックの正しさが立証されることもあった。δ 関数もそのうちの1つである。
δ 関数が登場した当初、「こんなもの数学ではない」と数学者には認めてもらえなかったのである。ところが、後にブルバギの一人、ローラン・シュワルツ(Schwarts;仏1915-2002)が超関数論を出すに及んで、δ 関数も数学の関数として認定された経緯がある。
ブルバギというのは工学関係者にはおそらく馴染みのない名前であろうが、数学関係者にはよく知られる名前である。個人名ではなく複数の数学者で結成された秘密結社の名前である。結成当初はフランス国内で広く使用されていたグルサ(Goursat;仏1858-1936)著の数学書が純数数学者仲間には不評であり(工学者にはむしろグルサの方が馴染あるかもしれないが)、新しいものを出版しようという計画から始まったものである。“1”の定義に200ページも費やしていると聞いては、われわれ工学者には近寄り難いものを感じるだろう。
ところで、シュワルツは20世紀の超一流数学者だっただけでなく政治運動の方面でも活躍した人物であり、昨年(2002)87歳で亡くなったところである。ご冥福を祈る。
[追記]
δ という記号はなかなか人気があるらしい。工学関係で使用する数学では他にクロネッカーの δ 関数がある(“理系夜話”第9話参照)。
2003年7月 記

